Ungleichseitiges Dreieck: Definition,Formel & Anwendung! [Ratgeber]

Haben Sie sich jemals gefragt, warum bestimmte Formen in der Natur und der Technik so häufig vorkommen? Die Antwort liegt oft in ihrer inhärenten Stabilität und Vielseitigkeit, Eigenschaften, die das ungleichseitige Dreieck perfekt verkörpert.

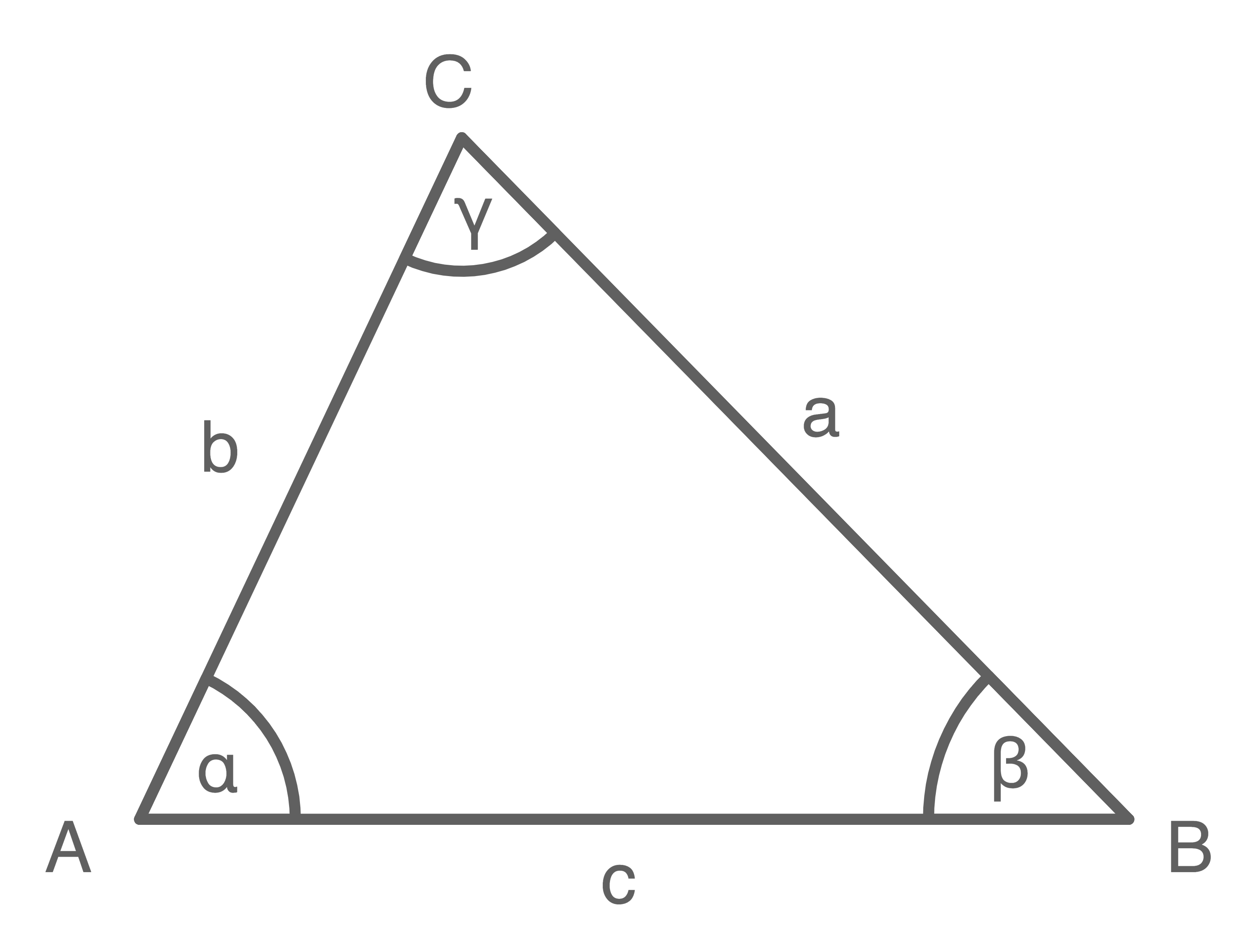
Das ungleichseitige Dreieck, auch als unregelmäßiges Dreieck bekannt, ist in der Geometrie ein faszinierendes Studienobjekt. Es zeichnet sich dadurch aus, dass alle drei Seiten unterschiedliche Längen aufweisen und somit auch alle drei Winkel verschieden groß sind. Im Gegensatz zu gleichseitigen Dreiecken (mit drei gleichen Seiten und Winkeln) oder gleichschenkligen Dreiecken (mit zwei gleichen Seiten und Winkeln) bietet das ungleichseitige Dreieck eine größere Vielfalt an Formen und Eigenschaften. Diese Vielfalt macht es zu einem wichtigen Werkzeug, um die grundlegenden Prinzipien der Geometrie zu verstehen und anzuwenden.

Die Analyse ungleichseitiger Dreiecke ermöglicht es uns, die Eigenschaften von Dreiecken ohne die Einschränkung gleicher Seiten oder Winkel zu untersuchen. Dies ist besonders nützlich, um das Konzept der Dreiecksungleichung zu erforschen, das besagt, dass die Summe der Längen zweier beliebiger Seiten eines Dreiecks immer größer sein muss als die Länge der dritten Seite. Nur so kann ein Dreieck überhaupt konstruiert werden. Die Untersuchung ungleichseitiger Dreiecke hilft auch dabei, Dreiecke in verschiedene Typen einzuteilen, basierend auf ihren Seitenlängen und Winkelgrößen.

• Barstow Ca Dein Umfassender Reisefhrer Infos
• Tunesien Kulinarische Reise Kstlichkeiten Dein Foodguide

Die Einteilung von Dreiecken nach Seitenlängen führt zu drei Hauptkategorien: unregelmäßige (ungleichseitige), gleichschenklige und gleichseitige Dreiecke. Betrachtet man die Winkel, so lassen sich Dreiecke in spitzwinklige (alle Winkel kleiner als 90°), rechtwinklige (ein Winkel genau 90°) und stumpfwinklige (ein Winkel größer als 90°) Dreiecke unterteilen. Ein ungleichseitiges Dreieck kann spitzwinklig, rechtwinklig oder stumpfwinklig sein, was seine Vielseitigkeit noch weiter unterstreicht.

Merkmal	Details
Definition	Ein Dreieck, bei dem alle drei Seiten unterschiedlich lang sind und alle drei Winkel unterschiedliche Maße haben.
Seitenlängen	Alle drei Seiten haben unterschiedliche Längen (a ≠ b ≠ c).
Winkel	Alle drei Winkel haben unterschiedliche Größen (α ≠ β ≠ γ).
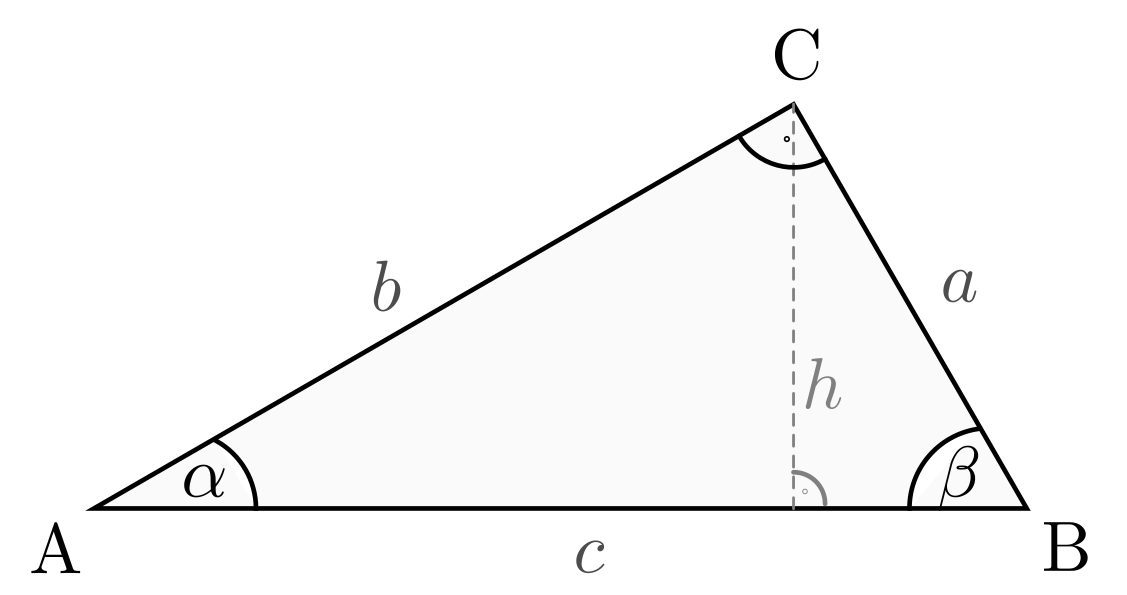
Höhe	Die Höhe eines ungleichseitigen Dreiecks ist der Abstand zwischen einer der Ecken und der Linie, die die gegenüberliegende Seite bildet. Es gibt drei verschiedene Höhen, abhängig von der gewählten Basis.
Flächenberechnung	Es gibt verschiedene Formeln zur Berechnung der Fläche, darunter die Heron-Formel: A = √[s(s-a)(s-b)(s-c)], wobei s der halbe Umfang ist (s = (a+b+c)/2) und a, b, c die Seitenlängen sind. Alternativ kann man A = (basis höhe) / 2 verwenden, wenn die Höhe bekannt ist.
Beispiele	Viele natürlich vorkommende und künstlich geschaffene Dreiecke sind ungleichseitig. Architektonische Strukturen, Brücken und Dächer nutzen oft ungleichseitige Dreiecke zur Stabilität und Gewichtsverteilung.
Verwendung	Studium von Dreieckseigenschaften, Erkundung der Dreiecksungleichung, Klassifizierung von Dreiecken, praktische Anwendungen in Architektur, Ingenieurwesen und Design.
Berechnungsformeln	Satz des Pythagoras (nur für rechtwinklige Dreiecke): a² + b² = c². Sinussatz: a / sin(α) = b / sin(β) = c / sin(γ). Kosinussatz: c² = a² + b² - 2ab cos(γ).
Zusätzliche Informationen	Ungleichseitige Dreiecke können spitzwinklig (alle Winkel < 90°), rechtwinklig (ein Winkel = 90°) oder stumpfwinklig (ein Winkel > 90°) sein.
Referenz	Easy-Schule Mathematik

Die Tatsache, dass ein ungleichseitiges Dreieck drei verschieden lange Seiten und drei verschieden große Winkel hat, bedeutet, dass es keine Symmetrie aufweist. Dies mag auf den ersten Blick als Nachteil erscheinen, ist aber in Wirklichkeit eine Quelle seiner Stärke. Die fehlende Symmetrie ermöglicht es dem Dreieck, sich an eine Vielzahl von Situationen anzupassen und in verschiedenen Anwendungen eingesetzt zu werden. Denken Sie an die Konstruktion von Brücken oder Dächern: Ungleichseitige Dreiecke können so gestaltet werden, dass sie spezifische Lasten tragen und Kräfte optimal verteilen. Sie sind das "Arbeitstier" unter den Dreiecken.

Die Berechnung der Fläche eines ungleichseitigen Dreiecks kann auf verschiedene Arten erfolgen. Eine gängige Methode ist die Verwendung der Heron-Formel, die nur die Längen der drei Seiten erfordert. Die Formel lautet: A = √[s(s-a)(s-b)(s-c)], wobei 'a', 'b' und 'c' die Seitenlängen sind und 's' der halbe Umfang des Dreiecks ist (s = (a+b+c)/2). Diese Formel ist besonders nützlich, wenn die Höhe des Dreiecks nicht bekannt ist. Alternativ kann die Standardformel für die Fläche eines Dreiecks (A = 1/2 Basis * Höhe) verwendet werden, wenn die Höhe bekannt ist. Da ein ungleichseitiges Dreieck keine offensichtliche "Basis" und "Höhe" hat, muss man unter Umständen eine der Seiten als Basis wählen und dann die entsprechende Höhe (die senkrechte Entfernung von der gegenüberliegenden Ecke zur Basis) berechnen.

• Miriam Mack Werdegang Advocacy Karriere Alles Wichtige
• Sa Foradada Mallorca Geheimtipp Restauranterlebnis

Die Winkel eines ungleichseitigen Dreiecks sind ebenfalls von Interesse. Da die Summe der Innenwinkel eines jeden Dreiecks immer 180° beträgt, kann man die Größe eines Winkels bestimmen, wenn die Größen der anderen beiden bekannt sind. Sind die Seitenlängen bekannt, kann man die Winkel mithilfe des Kosinussatzes berechnen. Der Kosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras und gilt für alle Dreiecke, nicht nur für rechtwinklige. Die Formel lautet: c² = a² + b² - 2ab cos(γ), wobei 'c' die Seite gegenüber dem Winkel 'γ' ist und 'a' und 'b' die anderen beiden Seiten sind. Durch Umstellen der Formel kann man den Winkel 'γ' berechnen, wenn die Seitenlängen 'a', 'b' und 'c' bekannt sind.

Ein wichtiges Konzept im Zusammenhang mit Dreiecken ist der Satz des Pythagoras, der jedoch nur für rechtwinklige Dreiecke gilt. Da ein ungleichseitiges Dreieck rechtwinklig sein kann, ist es wichtig zu verstehen, wann der Satz des Pythagoras anwendbar ist und wann nicht. Der Satz besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Länge der Hypotenuse (der Seite gegenüber dem rechten Winkel) gleich der Summe der Quadrate der Längen der beiden anderen Seiten ist (a² + b² = c²). Wenn ein ungleichseitiges Dreieck also einen rechten Winkel hat, kann der Satz des Pythagoras verwendet werden, um Beziehungen zwischen den Seitenlängen herzustellen.

Neben dem Satz des Pythagoras sind auch der Sinussatz und der Kosinussatz wichtige Werkzeuge zur Analyse von Dreiecken, einschließlich ungleichseitiger Dreiecke. Der Sinussatz besagt, dass das Verhältnis der Länge einer Seite zum Sinus des gegenüberliegenden Winkels für alle drei Seiten des Dreiecks gleich ist (a / sin(α) = b / sin(β) = c / sin(γ)). Der Kosinussatz, wie bereits erwähnt, ermöglicht die Berechnung von Winkeln, wenn die Seitenlängen bekannt sind, oder die Berechnung einer Seitenlänge, wenn die anderen beiden Seitenlängen und der gegenüberliegende Winkel bekannt sind. Diese Sätze sind besonders nützlich, wenn man mit nicht-rechtwinkligen Dreiecken arbeitet.

Die Anwendungen ungleichseitiger Dreiecke sind vielfältig und reichen von der Architektur und dem Ingenieurwesen bis hin zur Kunst und dem Design. In der Architektur werden sie zur Konstruktion von Dächern, Brücken und anderen Strukturen verwendet, bei denen Stabilität und Gewichtsverteilung von entscheidender Bedeutung sind. Die unterschiedlichen Winkel und Seitenlängen ermöglichen es den Designern, Strukturen zu schaffen, die spezifische Lasten tragen und Kräfte optimal verteilen. Im Ingenieurwesen werden ungleichseitige Dreiecke zur Analyse von Spannungen und Belastungen in verschiedenen Materialien und Strukturen eingesetzt. In der Kunst und im Design werden sie verwendet, um interessante und dynamische Kompositionen zu schaffen, die das Auge des Betrachters fesseln.

Die Klassifizierung von Dreiecken nach ihren Winkeln ist ein weiterer wichtiger Aspekt der Geometrie. Ein spitzwinkliges Dreieck hat alle drei Winkel kleiner als 90°, ein rechtwinkliges Dreieck hat einen Winkel von genau 90°, und ein stumpfwinkliges Dreieck hat einen Winkel größer als 90°. Ein ungleichseitiges Dreieck kann jede dieser Kategorien sein, was seine Anpassungsfähigkeit und Vielseitigkeit weiter unterstreicht. Um festzustellen, ob ein ungleichseitiges Dreieck spitzwinklig, rechtwinklig oder stumpfwinklig ist, kann man die Quadrate der Seitenlängen vergleichen. Wenn a² + b² > c² (wobei 'c' die längste Seite ist), dann ist das Dreieck spitzwinklig. Wenn a² + b² = c², dann ist das Dreieck rechtwinklig. Und wenn a² + b² < c², dann ist das Dreieck stumpfwinklig.

Die Berechnung des Umfangs eines ungleichseitigen Dreiecks ist relativ einfach: Man addiert einfach die Längen aller drei Seiten (U = a + b + c). Im Gegensatz dazu ist die Berechnung der Fläche etwas komplizierter, da sie die Verwendung der Heron-Formel oder die Kenntnis der Höhe erfordert. Die Heron-Formel ist besonders nützlich, wenn die Höhe nicht bekannt ist, da sie nur die Seitenlängen benötigt. Die Formel lautet: A = √[s(s-a)(s-b)(s-c)], wobei 's' der halbe Umfang ist (s = (a+b+c)/2) und 'a', 'b' und 'c' die Seitenlängen sind.

Das Zeichnen eines ungleichseitigen Dreiecks ist eine grundlegende Fähigkeit in der Geometrie. Man kann entweder mit drei gegebenen Seitenlängen beginnen oder mit zwei Seitenlängen und dem eingeschlossenen Winkel. Wenn man drei Seitenlängen gegeben hat, kann man ein Lineal und einen Zirkel verwenden, um das Dreieck zu konstruieren. Man beginnt, indem man eine der Seiten als Basis zeichnet. Dann stellt man den Zirkel auf die Länge einer der anderen Seiten ein und zeichnet einen Kreisbogen von einem Ende der Basis. Anschließend stellt man den Zirkel auf die Länge der verbleibenden Seite ein und zeichnet einen Kreisbogen vom anderen Ende der Basis. Der Schnittpunkt der beiden Kreisbögen ist der dritte Eckpunkt des Dreiecks. Wenn man zwei Seitenlängen und den eingeschlossenen Winkel gegeben hat, kann man ein Lineal und einen Winkelmesser verwenden, um das Dreieck zu konstruieren. Man beginnt, indem man eine der Seiten als Basis zeichnet. Dann verwendet man den Winkelmesser, um den gegebenen Winkel am einen Ende der Basis zu konstruieren. Anschließend zeichnet man die zweite Seite entlang der konstruierten Linie. Der Endpunkt der zweiten Seite ist der dritte Eckpunkt des Dreiecks.

Das Verständnis ungleichseitiger Dreiecke ist nicht nur für die Geometrie wichtig, sondern auch für viele andere Bereiche der Mathematik und der Wissenschaft. Sie sind grundlegende Bausteine für komplexere geometrische Formen und spielen eine wichtige Rolle bei der Lösung von Problemen in der Trigonometrie, der Physik und dem Ingenieurwesen. Durch das Studium ungleichseitiger Dreiecke können wir ein tieferes Verständnis der Welt um uns herum entwickeln und unsere Fähigkeit verbessern, Probleme zu lösen und innovative Lösungen zu entwickeln.

Abschließend lässt sich sagen, dass das ungleichseitige Dreieck, obwohl es auf den ersten Blick unscheinbar wirken mag, ein faszinierendes und vielseitiges Studienobjekt in der Geometrie ist. Seine fehlende Symmetrie und seine Fähigkeit, verschiedene Formen anzunehmen, machen es zu einem wichtigen Werkzeug für die Untersuchung grundlegender geometrischer Prinzipien und für die Anwendung in einer Vielzahl von realen Anwendungen. Von der Architektur und dem Ingenieurwesen bis hin zur Kunst und dem Design spielen ungleichseitige Dreiecke eine entscheidende Rolle bei der Gestaltung unserer Welt.

Detail Author:

• Name : Prof. Lew Johns Jr.
• Username : dietrich.lorena
• Email : ava.halvorson@gmail.com
• Birthdate : 1999-09-24
• Address : 49060 Block Terrace Suite 760 West Rowan, RI 25059-3504
• Phone : 1-520-559-2612
• Company : Koepp-Dietrich
• Job : Spraying Machine Operator
• Bio : Accusamus voluptatum et aspernatur qui et. Eum atque rerum necessitatibus incidunt soluta atque. Error nulla et sapiente est sint hic quia. Facilis voluptates porro nihil molestias fuga et eos.

Socials

tiktok:

• url : https://tiktok.com/@ccormier
• username : ccormier
• bio : Neque voluptatem deleniti architecto ut fugiat ad repellendus.
• followers : 2110
• following : 342

facebook:

• url : https://facebook.com/cormier1978
• username : cormier1978
• bio : Similique blanditiis eos est sint excepturi sed hic.
• followers : 1089
• following : 2221

instagram:

• url : https://instagram.com/cormier2003
• username : cormier2003
• bio : Ab dolore et et quaerat impedit sapiente sed. Rerum ullam facere animi nesciunt accusantium non et.
• followers : 4699
• following : 2232